Madden – Julian Oscillation (MJO) Part-II
Madden–Julian Oscillation Life Cycle and Phase Diagram
Analysis and Reconstructed Codes by Sandro Lubis Graduate Student of Leipzig Institute for Meteorology, University of Leipzig, Germany
All computations are made using[ NCAR Command Language (NCL)]
September, 2012
—
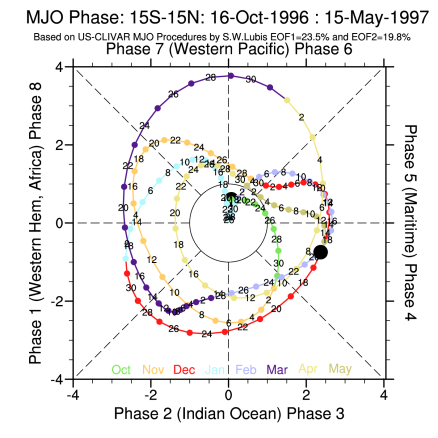
The Madden-Julian Oscillation (MJO) is the leading mode of intra-seasonal variability in the tropical troposphere, characterized by an eastward moving ‘pulse’ of cloud and rainfall near the equator that persists from weekly to monthly timescales. The following analysis follows the standard procedures of investigation MJO defined by US MJO Clivar WG. Generally, there are two main diagnostics steps pointed out by MJO Clivar WG, Waliser et al., 2009: Level 1: These diagnostics are meant to provide a basic indication of the spatial and temporal intraseasonal variability that can be easily understood and/or calculated by the non-MJO expert. These diagnostics include assessing variance in preferred frequency bands, spectral analysis over key domains, univariate empirical orthogonal function (EOF) analysis of bandpass filtered data, statistical significance assessment of the EOFs, and lead-lag assessment of the dominant intraseasonal principal component (PC) time series. Level 2: Diagnostics that provide a more comprehensive diagnosis of the MJO through multivariate EOF analysis and frequency wave-number decomposition.
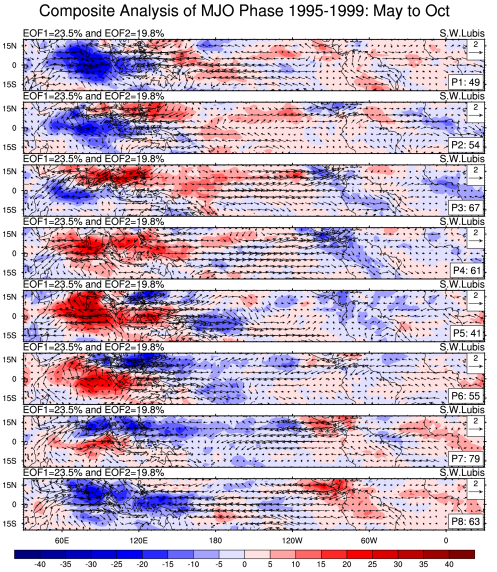
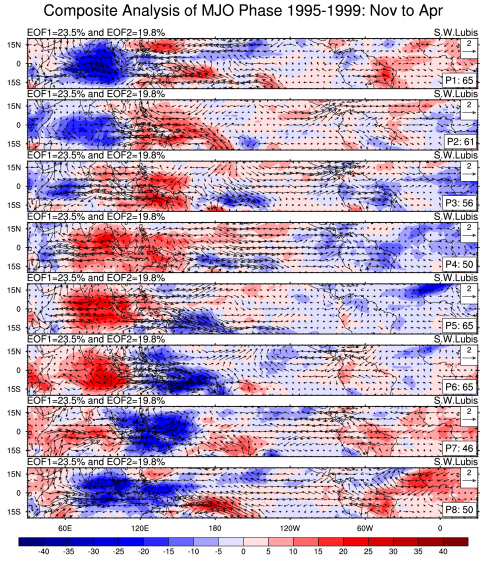
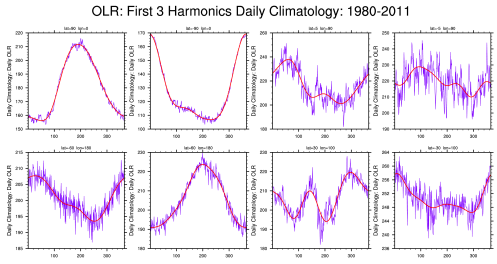
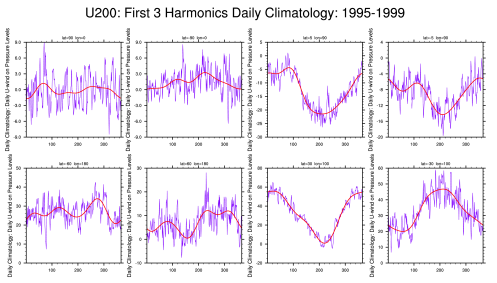
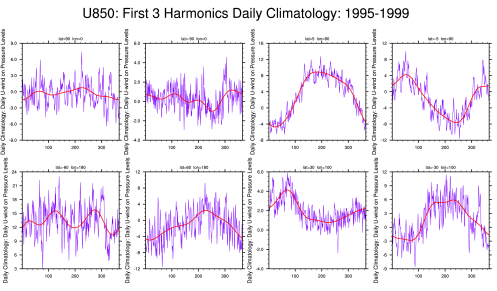
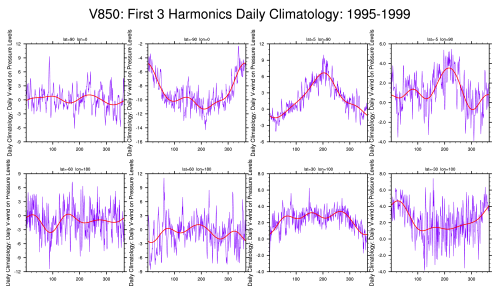
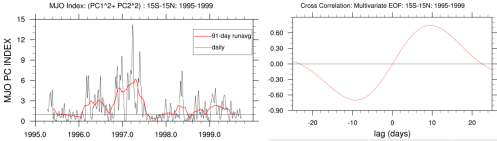
Data used in this analysis was retrieved from NOAA Reanalysis-II datasets consist of three main components: OLR, U200, and U850. V850 is also required for composite analysis of MJO. The daily anomalies are calculated using the first 3 harmonics of the seasonal cycle for 1980–2011. Afterwards, the band pass filter has been applied to these original anomalies. Compute the zonal mean of the temporal variance in order to normalize the variances. Then, compute combined EOF and normalize the multivariate EOF 1&2 component time series. Indices (multivariate MJO index) are obtained by computing (PC1^2+PC2^2).