Madden – Julian Oscillation (MJO) Part-I

Filtering Techniques for Monitoring the Madden–Julian Oscillation

Reconstructed Codes by Sandro Lubis 
Graduate Student of Leipzig Institute for Meteorology, University of Leipzig, Germany

All computations are made using
[ NCAR Command Language (NCL)] 

September, 2012

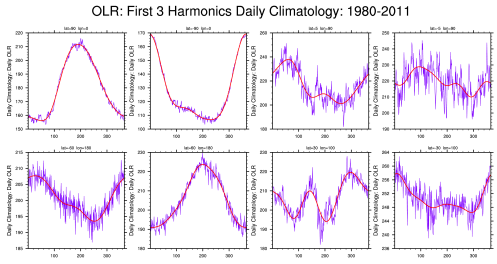
In this experiment,  Seasonal cycle is  removed by subtracting the first three harmonics of the annual cycle. It is done by following this common procedure: (1) perform an FFT to get real and imaginary coefficients. (2) arbitrarily retain the 1st ‘nHarm’ coefficients. No change in coefficients. (3) set the (nHarm+1) real and imaginary coefficientsto 0.5 of the original values. Set all others to 0.0. Presumably these are high frequency noise. (4) Do a back transform with coefficients as described in (3) . In this case, anomalies are calculated from Smooth Daily Climatology. Annual cycle that contains more harmonics will more closely resemble the actual data. Data was retrieved OLR NOAA from 1980-2011. In order to obtain obvious phenomenon of MJO , filtering technique  in time (20-100 days) and in space-time (k=1-5, 20-100d, Kiladis et all, 2009) are implemented. Missing values are linearly interpolated.

In order to test the reliability of the filter, the specific period was selected in which the phenomenon MJO was clearly visible. 2d FFT technique has been applied to see the direction of propagation of these oscillations.

Filter results in space and time (STSA)  as well as in time (BPF) are shown in the panel diagram below. In general, both filters have almost the same capabilities in isolating OLR anomalies associated with the MJO phenomenon. Filters in space and time  gives a smoother contour and more visible compared to the filter that only applied in time.

–Sandro Lubis–

~ by sandrolubis on September 11, 2012.